Two-step equations are fundamental algebraic expressions requiring two operations to solve. They involve variables and constants, teaching essential problem-solving skills and logical reasoning.
1.1; Definition and Importance of Two-Step Equations
Two-step equations are algebraic expressions that require two distinct operations to isolate the variable. They are essential for developing problem-solving skills and logical reasoning. These equations are widely used in real-world applications, such as financial planning and scientific calculations, making them a crucial part of foundational math education. Solving two-step equations helps students understand the relationship between variables and constants, preparing them for more complex algebraic concepts. Their importance lies in their ability to simplify everyday problem-solving and provide a strong base for advanced mathematical thinking.
1.2. Brief Overview of Algebraic Equations
Algebraic equations are statements that express the equality of two mathematical expressions, often involving variables and constants. They form the core of algebra, enabling the solution of unknown values through systematic operations. These equations can be linear or nonlinear, depending on the degree of the variable. Solving algebraic equations develops critical thinking and problem-solving skills, essential for various fields like science, engineering, and finance. They also serve as a foundation for more complex mathematical concepts, such as quadratic equations and systems of equations. Understanding algebraic equations is vital for manipulating and analyzing data, making them a cornerstone of modern mathematics and problem-solving methodologies.

Understanding the Structure of 2-Step Equations
Two-step equations involve variables and constants, solved using two operations. They require a clear understanding of algebraic principles and sequential problem-solving strategies to isolate the variable effectively.
2.1. Basic Components of a Two-Step Equation
A two-step equation consists of a variable and constants, requiring two operations to solve. It typically involves addition, subtraction, multiplication, or division on both sides. The structure includes a variable term and a constant term, often separated by an equal sign. These equations may involve combining like terms or applying inverse operations to isolate the variable. Understanding the components, such as coefficients and constants, is essential for effective problem-solving. Properly identifying these elements ensures accurate manipulation of the equation to find the variable’s value. Mastery of these components is foundational for advancing in algebra and solving more complex equations.
2.2. Identifying Variables and Constants
In two-step equations, variables represent unknown values, while constants are known numerical values. Variables are typically denoted by letters like x, y, or n, and constants are numbers without variables. Identifying these elements is crucial for solving equations accurately. For instance, in the equation 2x + 5 = 11, x is the variable, and 2 and 5 are constants. Recognizing the difference between variables and constants helps in applying appropriate operations to isolate the variable. This fundamental skill is essential for building a strong foundation in algebra and solving more complex equations effectively.
2.3. Balancing Equations: A Key Principle
Balancing equations ensures fairness and accuracy in solving algebraic problems. It involves performing the same operation on both sides of the equation to maintain equality. For example, if you add or subtract a number from one side, you must do the same to the other. This principle is vital for isolating variables and finding their values. Without balancing, equations lose their equality, leading to incorrect solutions. Always applying operations equally ensures that the equation remains true throughout the solving process. This fundamental rule is essential for building trust in mathematical outcomes and is a cornerstone of algebraic problem-solving.
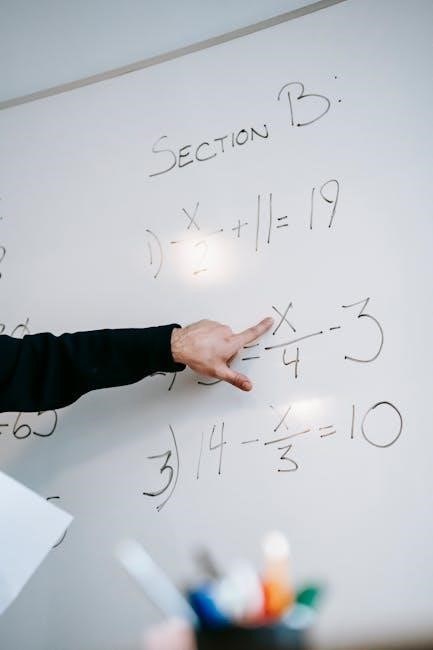
Strategies for Solving 2-Step Equations
Solving 2-step equations involves combining like terms, using inverse operations, and applying the distributive property. These strategies help isolate variables efficiently, ensuring accurate solutions;
3.1. Combining Like Terms
Combining like terms is a crucial step in simplifying two-step equations. This involves adding or subtracting coefficients of the same variable, such as 3x and 2x, to form 5x. By eliminating redundant terms, equations become easier to solve. For instance, in the equation 4x + 5 ౼ 2x = 11, combining 4x and -2x yields 2x + 5 = 11. This step ensures that the equation is streamlined, making it simpler to isolate the variable using inverse operations. Properly combining like terms is essential for maintaining the balance and integrity of the equation, leading to accurate solutions.
3.2. Using Inverse Operations
Using inverse operations is a fundamental strategy in solving two-step equations. Inverse operations are pairs of actions that reverse each other, such as addition and subtraction or multiplication and division. After combining like terms, the next step is to isolate the variable by applying the inverse operation. For example, in the equation (2x + 5 = 11), the inverse of adding 5 is subtracting 5, and the inverse of multiplying by 2 is dividing by 2. Applying these operations to both sides ensures the equation remains balanced. Mastery of inverse operations is essential for accurately solving two-step equations and maintaining mathematical integrity throughout the process.
3.3. The Role of the Distributive Property
The distributive property is a critical tool in solving two-step equations, especially when dealing with expressions involving parentheses. It allows you to simplify complex terms by distributing a number or variable across the terms inside the parentheses. For example, in the equation 3(x + 4) = 21, the distributive property helps expand it to 3x + 12 = 21. Once the equation is simplified, you can then apply inverse operations to solve for the variable. Proper use of the distributive property ensures that the equation remains balanced and leads to accurate solutions. This property is foundational for advancing to more complex algebraic problems.

Real-World Applications of 2-Step Equations
Two-step equations are essential in budgeting, cooking, and science, helping calculate costs, mix ingredients, and solve for variables in practical, everyday scenarios.
4.1. Financial Planning and Budgeting
Two-step equations are invaluable in financial planning and budgeting, enabling individuals to calculate total costs, allocate resources, and manage expenses effectively. For instance, determining the total price of a pizza, including toppings and delivery, or budgeting income and expenses, requires solving equations with multiple operations. These equations help in creating balanced budgets, ensuring financial stability, and making informed purchasing decisions. By applying algebraic principles, individuals can efficiently track and control their finances, making two-step equations a practical tool for everyday money management and long-term financial planning.
4.2. Scientific Calculations
Two-step equations are essential in scientific calculations, where precise solutions are critical. In fields like physics and engineering, these equations model phenomena such as motion and energy transfer. For example, calculating velocity or force often involves two operations, ensuring accuracy in experiments and simulations. They are also used in solving Cauchy problems and evolution equations, fundamental in understanding dynamic systems. By applying two-step equations, scientists and researchers can break down complex problems into manageable parts, leading to reliable and reproducible results. This methodological approach enhances problem-solving in various scientific disciplines, making two-step equations a cornerstone of analytical techniques in modern science.
4.3. Everyday Problem Solving
Two-step equations are practical tools for everyday problem solving, aiding in budgeting, cooking, and time management. For instance, calculating total costs or adjusting recipes involves combining like terms and applying inverse operations. These equations help in splitting bills evenly among friends or determining travel distances. They also assist in managing personal finances, such as calculating savings or interest. By breaking down real-life scenarios into simple steps, two-step equations empower individuals to make informed decisions efficiently. Their versatility makes them indispensable in navigating various daily challenges, transforming abstract math into a useful skill for all.

Common Mistakes and Misconceptions
Common errors include forgetting to apply operations to both sides, misapplying order of operations, and incorrect simplification, leading to wrong solutions and algebraic misunderstandings.
5.1. Forgetting to Apply Operations to Both Sides
One of the most common mistakes when solving 2-step equations is forgetting to apply operations to both sides of the equation. This often leads to incorrect solutions. For example, if a student adds 5 to one side but neglects to do the same on the other, the equation becomes unbalanced. This error can occur due to rushing or lack of attention to detail. It is crucial to remember that algebraic expressions require balance, meaning any operation performed on one side must also be applied to the other. Without this step, the variable cannot be isolated correctly. Always double-check work to avoid this pitfall and ensure the equation remains valid throughout the solving process. This mistake highlights the importance of careful execution in algebraic manipulations.
5.2. Misapplying the Order of Operations
Misapplying the order of operations is another frequent error in solving 2-step equations. Many students mistakenly perform operations out of sequence, leading to incorrect solutions. For instance, if an equation involves both multiplication and addition, failing to prioritize multiplication first can significantly alter the result. This error often stems from a lack of understanding of PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). To avoid this, always follow the proper sequence of operations and simplify expressions step by step. Double-checking work can help identify such mistakes early. Properly applying the order of operations ensures accuracy and builds a strong foundation in algebraic problem-solving. Consistent practice helps minimize this common pitfall.
5.3. Simplifying Incorrectly
Simplifying incorrectly is a common mistake when solving 2-step equations. This often occurs when combining like terms or handling negative signs improperly. For example, students might incorrectly combine coefficients or overlook the need to distribute negative signs to all terms within parentheses. Such errors can lead to incorrect solutions and hinder progress in algebra. To avoid this, it’s essential to work step by step, carefully simplifying each part of the equation. Double-checking each operation ensures accuracy. Proper attention to detail, such as handling negative signs correctly and combining like terms appropriately, is crucial. Practicing consistent simplification techniques builds confidence and reduces errors in solving 2-step equations.

Practice Problems and Worksheets
Downloadable PDF guides offer 10 two-step equation problems for practice, covering integers and variables like n. These worksheets are ideal for pre-algebra students and homeschooling.
6.1. Solving for Variables
Practice problems in PDF guides focus on solving for variables in two-step equations. These exercises involve integers and variables like ‘n,’ offering clear examples for pre-algebra students. Worksheets provide structured problems to build foundational skills, ensuring mastery of inverse operations and combining like terms. Each problem requires logical thinking and step-by-step execution, making them ideal for classroom or homeschool use. Solving for Variables sections in these guides help learners understand the importance of applying operations correctly to isolate the variable, reinforcing algebraic principles essential for advanced math. Regular practice with these problems enhances problem-solving abilities and confidence in handling equations.
6.2. Word Problems Involving Two-Step Equations
Word problems in two-step equations PDF guides apply algebraic concepts to real-life scenarios. These problems involve setting up equations based on descriptions and solving them step-by-step. For example, calculating total costs or distances using variables. Worksheets often include practical situations like budgeting or mixing ingredients, requiring students to interpret context and translate it into equations. Solving such problems enhances critical thinking and bridges abstract math to tangible applications. PDF resources provide clear examples and exercises, helping learners master the transition from words to algebraic expressions and solutions. These exercises are essential for developing problem-solving skills in everyday and academic contexts.
6.3. Mixed Operations in Equations
Mixed operations in two-step equations involve combining addition, subtraction, multiplication, and division within a single problem. These equations require careful application of the order of operations to ensure accuracy. For example, solving for a variable in an equation like ( 3x + 4 = 11 ) involves first subtracting 4 from both sides, then dividing by 3. PDF guides often include practice problems that mix these operations, helping students refine their algebraic skills. Mastering mixed operations is essential for tackling more complex equations and real-world applications, as they simulate scenarios requiring multiple steps to reach a solution.
Resources for Learning 2-Step Equations
Discover a variety of learning resources, including PDF guides, online tutorials, and interactive tools, designed to simplify mastering two-step equations through step-by-step instructions and practical exercises.
7.1. Recommended PDF Guides
Enhance your understanding of two-step equations with recommended PDF guides offering detailed explanations, practice problems, and solutions. These resources, such as “Two-Step Equations HW” and “2 Step Equations Worksheet,” provide structured lessons and exercises to master algebraic concepts. Many guides are free to download and include step-by-step instructions, making them ideal for self-study or classroom use. They often cover topics like solving for variables, word problems, and mixed operations, catering to different learning styles. Whether you’re a student or educator, these PDFs are invaluable tools for building a strong foundation in algebra and improving problem-solving skills through practical application.
7.2. Online Tutorials and Videos
Online tutorials and videos are excellent resources for mastering two-step equations. Platforms like YouTube and educational websites offer step-by-step guides, making complex concepts easy to grasp. Many channels provide interactive examples, allowing learners to follow along and practice simultaneously. Videos often cover topics like solving for variables, word problems, and mixed operations, catering to diverse learning styles. Some tutorials even include quizzes or exercises with immediate feedback, enhancing engagement and understanding. These resources are particularly helpful for visual learners, as they combine audio and visual explanations. Additionally, specialized math channels, such as Khan Academy, offer in-depth lessons tailored for different skill levels. This accessibility makes online tutorials a valuable supplement to traditional study materials, ensuring learners can reinforce their knowledge anytime, anywhere.
7.3. Interactive Tools and Calculators
Interactive tools and calculators provide hands-on practice for solving two-step equations. Online platforms offer equation solvers that allow users to input problems and receive step-by-step solutions. These tools often include features like graphing capabilities, algebraic manipulation, and real-time feedback. Many calculators are designed with user-friendly interfaces, making them accessible for learners of all levels. Some tools even provide interactive lessons, combining instruction with practice exercises. They cater to visual and kinesthetic learners by enabling experimentation with different variables and constants. Resources like Desmos and Symbolab are popular choices, offering comprehensive support for understanding and mastering two-step equations. These tools are invaluable for reinforcing concepts and building confidence in problem-solving skills.

Advanced Topics Related to 2-Step Equations
Exploring systems of equations, quadratic equations, and fractional equations builds on the foundation of two-step equations, introducing complexity and deeper algebraic problem-solving techniques.

8.1. Systems of Equations
Systems of equations involve solving multiple equations simultaneously, often requiring advanced techniques beyond two-step equations. These systems can include linear or nonlinear equations and are commonly solved using substitution or elimination methods. In the context of two-step equations, understanding systems lays the groundwork for tackling real-world problems that involve multiple variables and complex relationships. For instance, financial planning might require solving for both savings and expenses, while scientific applications could involve balancing multiple unknowns in an experiment. Mastery of systems of equations enhances analytical skills and prepares learners for higher-level mathematics and practical problem-solving scenarios.
8.2. Quadratic Equations
Quadratic equations are polynomial equations of degree two, characterized by a squared variable, typically in the form of ( ax^2 + bx + c = 0 ). Unlike two-step equations, solving quadratics often requires advanced methods such as factoring, completing the square, or applying the quadratic formula. These equations are crucial in various fields, including physics, engineering, and economics, where modeling real-world phenomena like projectile motion or economic growth is essential. Resources like PDF guides and online tutorials provide detailed steps for solving quadratic equations, emphasizing their importance in progressing from basic algebra to more complex problem-solving. Mastering quadratics builds a strong foundation for advanced mathematical studies and practical applications.
8.3. Fractional and Decimal Equations
Fractional and decimal equations introduce variables with non-integer coefficients, adding complexity to two-step problems. Solving these requires precision, as improper handling of fractions or decimals can lead to inaccuracies. Resources like PDF guides provide step-by-step methods for such equations, emphasizing techniques like clearing denominators or converting decimals to fractions. These equations are common in scientific and financial calculations, where exactness is critical. Practicing with specialized worksheets helps build confidence and accuracy, ensuring mastery of these challenging algebraic expressions.

Case Studies and Examples
Real-life scenarios and historical problems illustrate practical applications of two-step equations, offering insights into their everyday relevance across various fields like finance, science, and engineering.
9.1. Real-Life Scenarios
Two-step equations are essential in real-life financial planning, such as calculating total costs for pizzas or budgeting expenses. They help in determining unknowns, like finding the cost per slice or total savings, by breaking down problems into manageable steps. For instance, if a pizza costs $9 and additional toppings add $2 each, solving a two-step equation reveals the total price. Similarly, in budgeting, equations can calculate remaining balances after expenses. These practical applications emphasize the importance of mastering two-step equations for everyday decision-making and problem-solving, making them a cornerstone of basic algebraic skills.
9.2. Historical Problems
Historically, two-step equations have been pivotal in solving various mathematical problems, showcasing their versatility. For instance, in the study of operator approximations by Akopian, two-step equations provided foundational methods for analyzing algebraic properties. Similarly, Vabishchevich’s work on approximate solutions for evolution equations highlights their enduring relevance. These equations have also been instrumental in solving systems of equations, as seen in financial and scientific contexts, where breaking down complex problems into simpler steps has been essential. The historical use of two-step equations underscores their importance in advancing mathematical theories and practical applications, demonstrating their timeless utility in problem-solving across disciplines.
9.3. Modern Applications
Two-step equations remain integral to modern problem-solving, with applications in engineering, physics, and finance. They are used to model real-world scenarios, such as calculating distances in motion problems or determining budgets. In STEM fields, these equations help solve systems of equations and optimize processes. For instance, in fluid dynamics, two-step equations are employed to analyze pressure and flow rates. Additionally, they are essential in computer science for algorithm design and data analysis. Their simplicity and versatility make them a cornerstone in educational curricula, preparing students for complex mathematical challenges. Modern tools, like interactive calculators, further enhance their application, ensuring they remain relevant in today’s fast-paced, technology-driven world.
Mastering two-step equations is essential for algebraic proficiency; With numerous PDF guides and online resources available, consistent practice ensures problem-solving skills and real-world application fluency.
10.1. Recap of Key Concepts
In solving two-step equations, combining like terms and applying inverse operations are crucial. The distributive property often simplifies expressions. Ensuring operations are applied to both sides maintains balance. Practice with PDF worksheets enhances fluency, while understanding real-world applications reinforces problem-solving skills. Mastery of these concepts builds a strong foundation for advanced algebra and practical problem-solving scenarios.
10.2. Encouragement for Further Practice
Consistent practice is essential for mastering two-step equations. Utilize PDF guides and worksheets to reinforce learning. Start with simple problems, gradually tackling more complex scenarios. Engage with online tools and interactive calculators for hands-on experience. Regular practice builds confidence and improves problem-solving skills. Apply these concepts to real-world situations, such as budgeting or scientific calculations, to see their practical value. Remember, proficiency in two-step equations is a foundational skill that enhances overall mathematical fluency and logical thinking.
10.3. The Importance of Mastery
Mastery of two-step equations is crucial for algebraic proficiency and problem-solving. It forms the basis for more complex mathematical concepts, such as quadratic and systems of equations. Understanding these principles enhances analytical thinking and logical reasoning. Proficiency in two-step equations is essential for various fields, including science, engineering, and finance. By mastering these equations, students develop a solid foundation for advanced mathematics and real-world applications. Regular practice with PDF resources and online tools ensures long-term retention and skill improvement, making it a valuable investment in educational and professional growth.
